Una definició de seguretat industrial estableix que «és un àrea multidisciplinària que s’encarrega de minimitzar els riscos en la indústria». Aquesta definició ens pot preocupar lleugerament, ja que no parla d’eliminar, sinó de minimitzar els riscos. I aquí és on trobem l’aplicabilitat de l’estadística en aquesta minimització de riscos, o l’intent d’aconseguir l’impossible risc zero. Els aspectes en què l’estadística pot col•laborar són:
- L’estadística descriptiva.
- L’estudi i aplicabilitat de models de variació de les dades.
- Les eines de control estadístic de processos.
Una de les tècniques més usades són els diagrames de causa-efecte d’Ishikawa, també anomenats d’espina de peix, que ajuden, en l’àmbit industrial, a detectar les causes que produeixen efectes no desitjats (Figura 1). Aquesta tècnica inclou sis categories principals, «les 6M»: mesures, material, mà d’obra, medi ambient o entorn, mètodes i màquines).
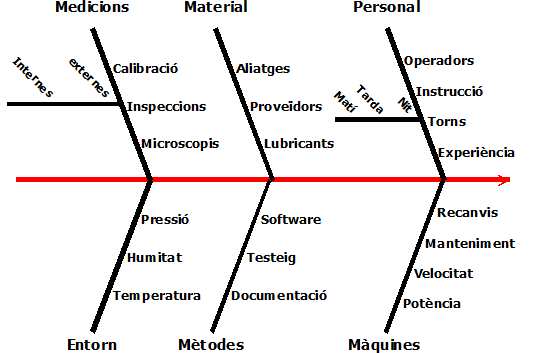
Figura 1. Exemple
de diagrama d’Ishikawa amb sis causes principals i algunes
subcauses.
En segon lloc, si assumim la premissa que els riscos, accidents o mals funcionaments es produeixen com a conseqüència d’una desviació de les variables de procés pel que fa als paràmetres normals d’operació en el nostre sistema en un moment donat, estem entrant en el terreny de l’estudi de models i la seva variabilitat. Tot i que som conscients que mai no elaborarem dos productes exactament iguals, ja que hi ha petites variacions degudes a l’atzar, les variacions grans –no atzaroses– són les que ens poden donar problemes de seguretat. Per a posar-ne un petit exemple, plantegem-nos un procés del qual observem una característica que segueix un funcionament basat en un model de distribució normal (Figura 2).
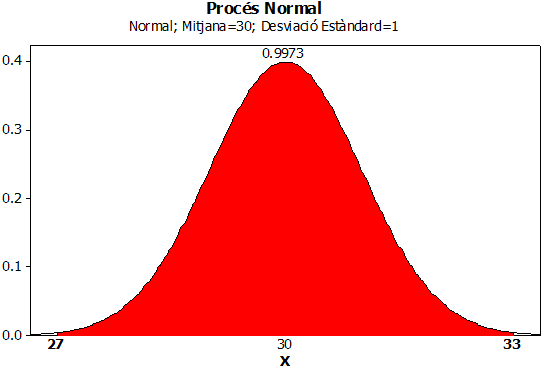
Figura 2. Densitat
normal amb l’àrea entre 27 i 33
remarcada.
Quan aquest procés està centrat a 30, ja sabem que la característica no serà sempre igual a 30, sinó que farem petites fluctuacions aleatòries amb valors propers a 30. Els problemes greus de seguretat poden ser detectats quan ens allunyem del centre. Per exemple, podem calcular, amb el model normal, la probabilitat d’estar a més de 3 desviacions unitàries, és a dir, la probabilitat d’estar per sota de 27 o d’estar per sobre de 33. Aquesta probabilitat és molt petita, 0,0027; és a dir, no arriba a 3 de cada 1.000 vegades. Però, per exemple, si aquesta és la probabilitat de cada dia de treball de la màquina, un altre model probabilístic –aquesta vegada el model binomial–, ens permet afirmar que la probabilitat que en un any no tinguem cap accident és només del 37,28 %.
L’ús d’aquests models serà el que ens donarà que la probabilitat de risc zero en la seguretat industrial és gairebé nul•la. Encara que tinguem una probabilitat molt i molt baixa de patir un risc, la repetició dia rere dia fa que l’esperança de risc augmenti. I podeu fer el joc de posar la probabilitat tan petita com vulgueu i multiplicar-ho per un nombre de vegades fins arribar a obtenir un producte igual a 1. Aquest nombre de vegades serà el de les repeticions que haurem de fer de mitjana fins que s’esdevingui la situació de risc, és a dir, de pèrdua de seguretat.
Finalment, l’avaluació dels riscos en la seguretat industrial no només es pot basar a identificar els riscos –deixant de banda les conseqüències o magnitud dels danys– i conèixer la probabilitat de tenir-los, sinó en el control estadístic de processos per veure que les condicions de seguretat es mantenen.
Hi ha moltes eines de control estadístic de processos; una de les més bàsiques són els gràfics de control. Amb aquestes tècniques podem seguir l’evolució del nostre procés industrial i detectar anomalies i intervenir en el procés. En els gràfics següents, anomenats Xbar (Figura 3), podem observar un procés sota control i un procés fora de control. Cada punt correspon a la mitjana d’una mostra en el temps, i els punts marcats en colors ens indiquen el trencament d’alguna de les regles de control i, per tant, possibles causes de risc i inseguretat.
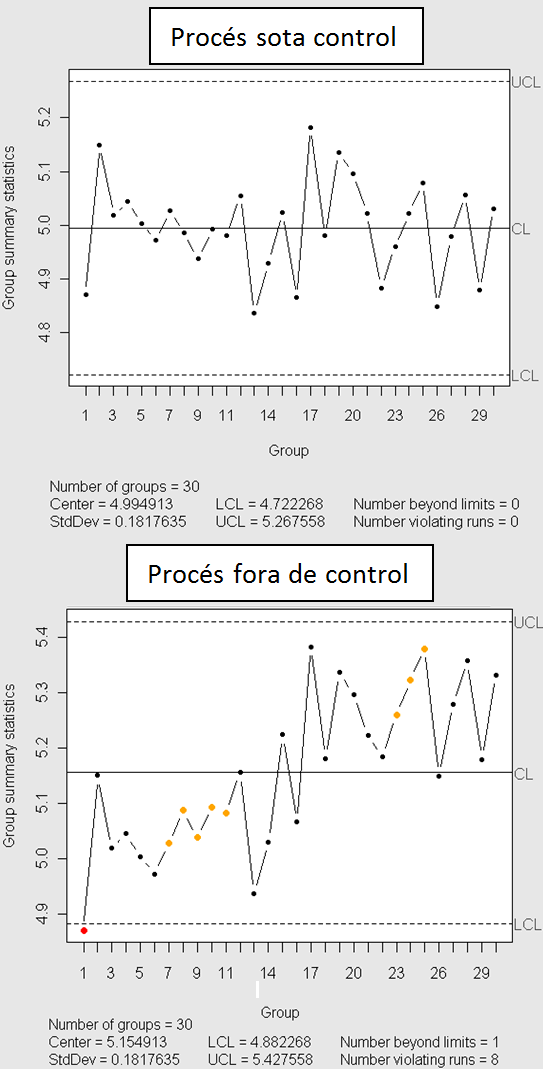
Figura
3. Gràfics Xbar d’un procés
sota control i d’un procés fora de control.
< TORNAR

