
| |
| Presentació |
| Continguts |
| Tecnologia |
| Docència |
| Recerca i transferència tecnològica |
| Estudiants |
| Professionals |
| Patronat |
| Activitats |

Recerca i transferència tecnològica
Equacions diferencials, modelització i aplicacions (EDMA)
Les equacions diferencials són el llenguatge amb què es descriuen els processos en ciència i enginyeria. Per comprendre aquests processos cal sempre una primera fase de descripció que, sovint, va seguida d’una segona fase de modelització matemàtica amb equacions diferencials. Des del clàssic problema del moviment dels planetes al voltant del Sol fins a l’estudi de la deformació d’estructures o del creixement de xarxes complexes com Internet, passant per l’estudi de la dinàmica de les no menys complexes xarxes metabòliques i de regulació genètica, tots aquests casos són modelitzats per equacions diferencials.
Dos dels objectius fonamentals de la recerca del grup Equacions Diferencials, Modelització i Aplicacions (EDMA) del Departament d’Informàtica i Matemàtica Aplicada de la UdG són el plantejament i l’anàlisi de nous models que descriguin processos biològics (dinàmica de poblacions, propagació d’epidèmies en xarxes complexes) i de l’enginyeria (disseny òptim de xarxes de transport), així com l’estudi del comportament de les solucions de models ja establerts, com per exemple les de la mecànica celeste.
Les línies principals de recerca del grup són: l’estudi de les xarxes complexes, la dinàmica de poblacions estructurades, la mecànica celeste i les aplicacions de les equacions diferencials.
Xarxes complexes
Des de fa relativament poc es comencen a tenir dades sobre algunes d’aquestes xarxes i, a més, prou capacitat computacional per estudiar l’ingent volum de dades que les descriuen. Això ha provocat que al final dels anys noranta sorgissin els primers models matemàtics per al creixement d’aquestes xarxes a mesura que nous elements s’hi van afegint. L’estudi de les propietats de l’arquitectura d’aquestes xarxes segons els diferents mecanismes de creixement és un dels objectius d’aquesta línia de recerca del grup.
Però les xarxes no només són objecte d’estudi per si mateixes, sinó que també defineixen el terreny de joc on tenen lloc diferents processos: transmissió d’informació, propagació d’energia, etc. Un dels casos més interessants és el de la propagació d’epidèmies en xarxes socials o de virus a Internet. En els models clàssics de l’epidemiologia, s’assumeix que tothom té contacte amb tothom a l’hora d’estudiar la propagació de malalties infeccioses. Aquest precepte va deixant pas cada cop més a la idea d’incloure l’estructura de les xarxes de contacte com un ingredient més dels models epidemiològics. L’anomenada epidemiologia en xarxes constitueix el segon tema d’estudi que ha iniciat recentment el nostre grup. Per exemple, el brot del SARS a la Xina el novembre del 2002 és una mostra de la importància del patró de contactes entre individus a l’hora de fer prediccions sobre una possible pandèmia. En aquest cas, les alarmistes prediccions inicials quan la malaltia va propagar-se a altres països com el Canadà —l’OMS va fer una alerta mundial el 15 de març de 2003— van quedar reduïdes a ben poca cosa quan, el juliol del 2003, l’epidèmia va quedar controlada (http://es.wikipedia.org/wiki/SARS).
Dinàmica de poblacions estructurades i dinàmica adaptativa
Quan s’estudien poblacions amb un cert nivell de detall, tant si són d’animals, de plantes o de polímers en processos de síntesi industrial, hom observa que tots els seus membres no són iguals: presenten diferències en edat, mida, rang social, nivell de reserves, etc. La descripció de la dinàmica d’aquestes poblacions estructurades per una o més variables internes es fa, generalment, mitjançant equacions en derivades parcials. L’estudi de les propietats de les solucions d’aquestes equacions és una de les línies de més tradició del grup i sobre la qual han fet la tesi tres dels nostres membres.
D’altra banda, conèixer les propietats de les equacions que descriuen la dinàmica de les poblacions estructurades té aplicacions molt importants en la gestió dels anomenats recursos naturals renovables, com són les pesqueries o les explotacions forestals, on una gestió sostenible dels recursos demana el coneixement de les implicacions que diferents tipus d’explotació poden tenir sobre el futur de les poblacions d’interès.
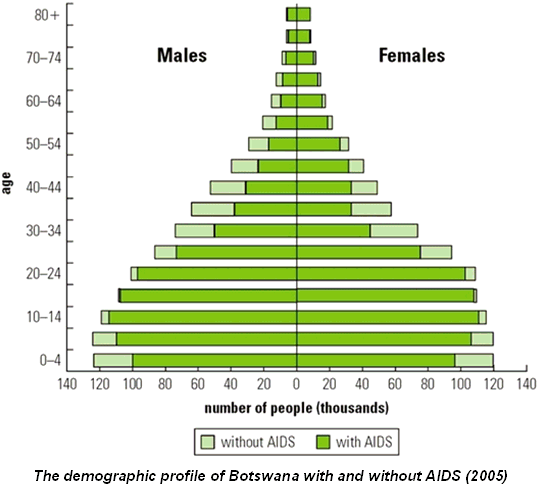
En el cas de poblacions biològiques, a més, el fet de tenir els individus estructurats per l’edat (o per la mida) permet formular de manera natural qüestions d’optimització del tipus “quina és l’edat òptima de maduració?”, “què és millor: fer A fins arribar a una mida M i després fer B, o fer-ho a l’inrevés? o fer-ho alhora però invertint cada vegada menys energia en una de les dues accions?”, “a quina edat és millor començar a vacunar per tal de prevenir un brot infecciós?” La teoria de jocs evolutius aplicada a aquest tipus de models de la dinàmica de poblacions constitueix el tercer gran tema de recerca d’aquesta línia. En aquest context, una estratègia és donada pel valor que pren un cert tret o característica fenotípica heretable, com per exemple l’edat de maduració. En particular, estem interessats en el càlcul de les anomenades estratègies evolutivament estables (o invencibles quan són adoptades per una majoria d’individus) per a diferents models de poblacions estructurades i característiques fenotípiques.
Mecànica celeste

Uns altres temes d’estudi dins l’astrodinàmica tenen a veure amb la determinació de trajectòries de conjunts de satèl•lits artificials, anomenats constel•lacions de satèl•lits, de manera que tots junts orbitin seguint una trajectòria nominal tot mantenint la seva posició relativa. En la figura, tenim una representació corresponent al projecte Darwin de l’Agència Espacial Europea i que té per objectiu trobar planetes semblants a la Terra.
Aplicacions
En els apartats anteriors s’ha posat de manifest l’interès dels membres del grup per les aplicacions de la seva recerca. En aquest sentit, cal destacar també altres àmbits ben diversos com ara els sistemes mecànics, la medicina o, fins i tot, el ball de competició, on ha participat la recerca del grup EDMA.
Sistemes mecànics amb dissipació:
A causa de la seva importància en l’enginyeria, els sistemes mecànics de suspensió-amortiment han estat objecte de recerca en el grup.
Trobem aquests sistemes, per exemple, en tot tipus de vehicles, però també formant part de l’estructura d’edificis, sobretot dels que estan situats en zones d’alt risc d’activitat sísmica. El model clàssic per a aquest tipus de sistemes (equació diferencial ordinària) no té en compte fenòmens com ara possibles diferències internes en la deformació de la molla, la pròpia dissipació interna del dispositiu o possibles controls externs per regular-ne l’estat. Això ens ha portat a un model d’equacions en derivades parcials per a aquest tipus de sistemes. El comportament asimptòtic (a llarg temps) de les solucions d’aquest model i la comparació amb l’enfocament clàssic formen part d’aquest estudi.

Modelització de la cicatrització de ferides: El procés de cicatrització d’una ferida és un fenomen ben natural, però també extremadament complex des del punt de vista bioquímic. Això fa que, malgrat la gran quantitat de recerca que generen, aquests mecanismes només s’entenguin de manera parcial i, a vegades, només s’analitzin des d’un punt de vista experimental. Durant els darrers anys, però, ha estat significativa l’aportació de la modelització matemàtica a l’estudi teòric d’aquests processos. Els models de les diferents fases que tenen lloc durant la cicatrització serveixen per entendre millor el funcionament dels mecanismes habituals, però també per analitzar altres aspectes més desconeguts, com ara els motius pels quals aquest procés falla en pacients amb certes malalties (la diabetis o les infeccions en són un exemple), i dóna lloc a problemes de cicatrització, com ara ferides cròniques. A més, la simulació numèrica d’aquests models també representa una eina magnífica a l’hora d’analitzar
l’eficàcia de nous tractaments.
Qualitat rítmica en el ball de competició:
L’objectiu d’aquest projecte és obtenir un mètode per mesurar la qualitat rítmica en el ball de competició, en què el ritme és un dels criteris utilitzats en la puntuació de les parelles de la competició.
Tot i la seva importància evident, doncs, la veritat és que el concepte de ritme no està tan clar com sembla i porta, per tant, a interpretacions subjectives. En aquest sentit, el projecte pretén donar objectivitat a aquest criteri: primer, analitzar què s’entén realment per ritme en el ball de competició i donar una representació matemàtica d’aquest concepte; i segon, dissenyar un mètode que a la pràctica permeti mesurar aquest ritme i comprovar-ne la qualitat. Tot això, sempre d’acord amb l’opinió dels experts.

Part de la recerca del grup estarà finançada el propers tres anys pel projecte del Ministeri anomenat Ecuaciones de evolución, redes complejas y dinámica de poblaciones. A més, els membres del grup EDMA també formen part d’altres grups de recerca d’universitats catalanes com el GREDPA (http://www-ma2.upc.edu/~edps/") o el Grup de Sistemes Dinàmics de la Universitat Autònoma de Barcelona (http://www.gsd.uab.es/). També en la direcció de les aplicacions, cal dir que membres del grup participen activament en els Grups d’Estudi de Matemàtica i Tecnologia (GEMT) (http://www-fme.upc.es/gemt/index.html). L’organització regular d’aquests Grups d’Estudi representa una oportunitat excel•lent per als investigadors, els industrials i els científics de diversos àmbits per interaccionar i comunicar-se, i permet així el sorgiment de noves col•laboracions entre el món de la matemàtica aplicada i la indústria.